Fractions - Proper, improper, and mixed
Concept
- There are three different types of fractions we come across commonly - proper, improper and mixed.
Theory
A proper fraction is one that’s less than 1, which seems very apt (because it is a “fracture” of a whole). In order for a fraction to be less than one the numerator has to be less than the denominator. Ex: 3/5.
An improper fraction is just the opposite - the numerator is greater than the denominator. This means an improper fraction is always greater than 1. Ex: 5/3
A mixed fraction is one that has whole number plus a fraction. Ex: 1 and 2/3. A mixed fraction is always greater than one.
An improper fraction can be converted into a mixed fraction and vice versa.
Converting fractions
A common task will be to convert an improper fraction to a mixed fraction. Because its odd to say 145/8, but easier to say 18 and 1/8ths.
To convert, simply divide the fraction using long division, and then you will arrive at the mixed fraction like so:
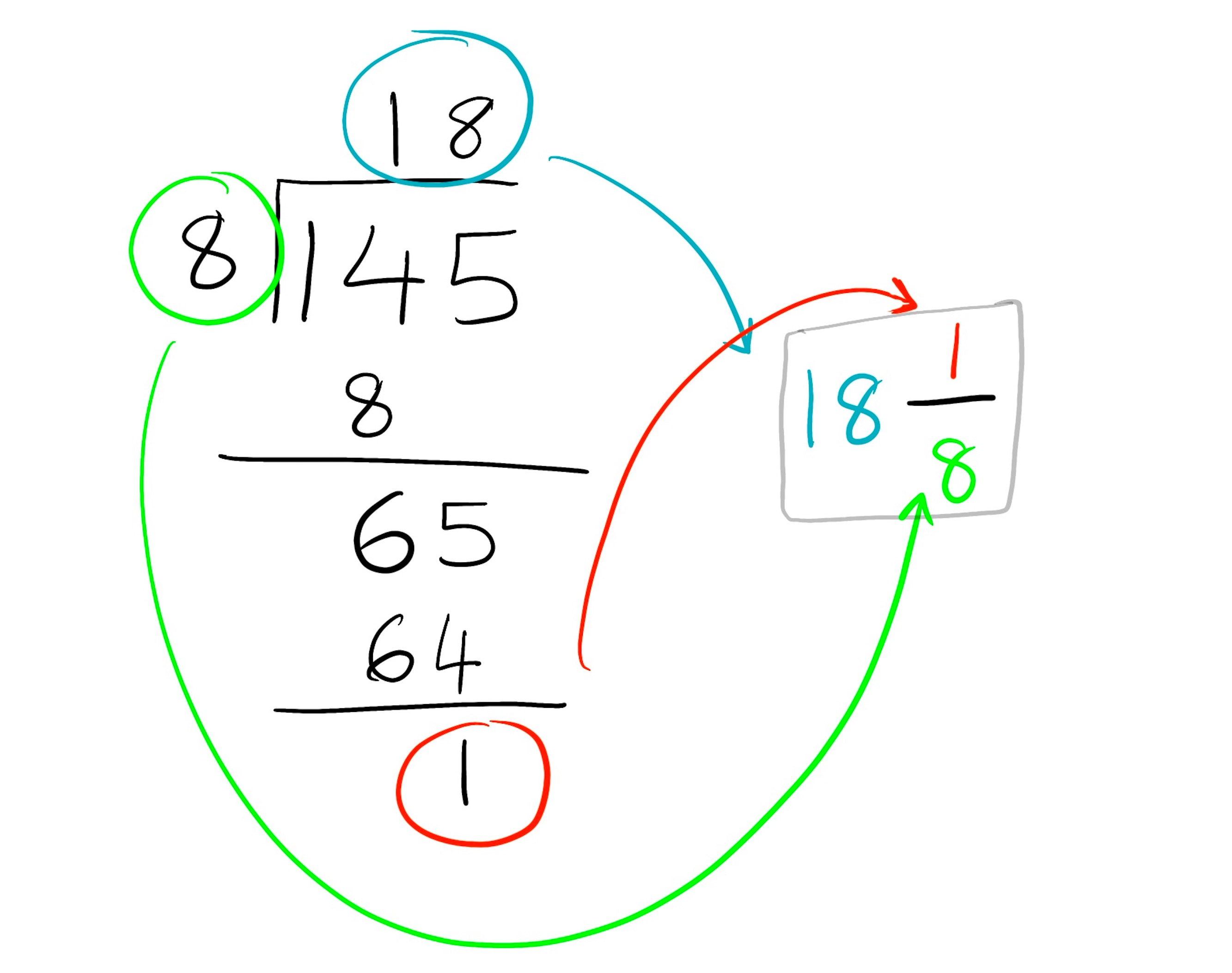
Here’s one more. To convert 232/12 into a mixed fraction, divide 232 by 12 to get the whole number part of the fraction, which is 19. Then, take the remainder (4) and divide it by 12 to get the fractional part of the fraction, which is 4/12. Therefore, the mixed fraction is 19 4/12.
Common Misconceptions
- Not understanding how to arrange the dividend, divisor and remainder when converting improper fractions to mixed fractions.