Ratio and Proportion
Concepts
Understand the meaning of:
- ratio
- proportion and their application in real life.
Theory
Ratio
A ratio is a way of comparing two or more quantities that are related to each other. It helps us understand how much of one thing we have compared to another thing. Let’s say there are two schools:
- School A has 1 teacher for 12 children.
- School B has 1 teacher for 40 children.
In math, we can say that the ratio of teacher: children is 1:12 for school A, and 1:40 for school B. Read the “:” as “is to.”
1 is to 12. 1 is to 40.
May sound weird, initially, but everything is, initially.
Proportion
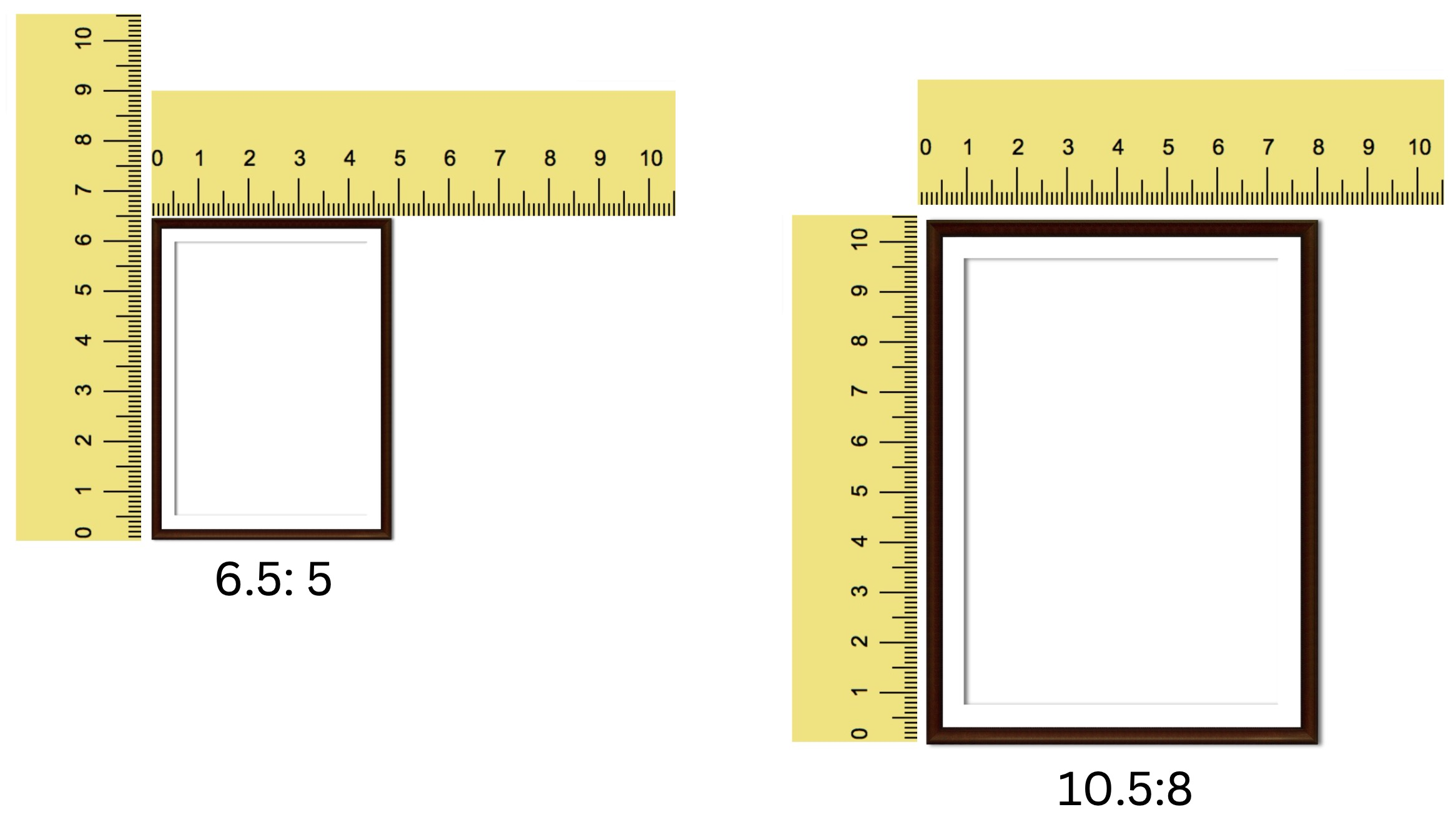
The two ratios are almost the same. 6.5/5 = 1.3 and 10.5/8 = 1.3. That is why both frames are said to be “proportionate”, or “in proportion.”
Remember, there will always to be two ratios, when we’re talking about proportion. Let’s you knew the dimensions of the first frame. And someone asked you to make a new frame, but with the length as 10.5cm instead. Would you be able to find out how wide you need to make the frame?
Yes, and the answer is via cross multiplication strategy.
If the two frames are to be in proportion then:
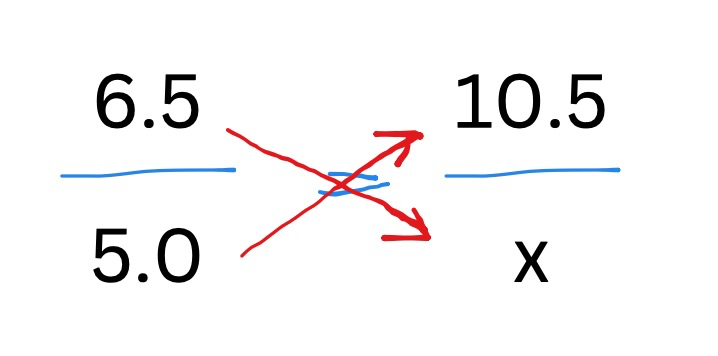
6.5 x X = 5.0 x 10.5 => X = (5.0 x 10.5)/6.5 => X = 8
And voila, you can be a proportionate frame maker with a little bit of knowledge of ratio and proportion.
Misconceptions
- Not quite a misconception, but while solving cross multiplication problems, students must be encouraged to simplify the fraction so they work with smaller numbers.